期望
期望存在一下特性:
1.
2.一般情况下,;当X和Y相互独立时,才有
在R中的代码实现:
set.seed(42)
x = rnorm(100)
x
# mean
x.mean = sum(x)/length(x)
x.mean
mean(x)
方差
方差描述的是随机变量的离散程度,也就是该变量离其期望值的距离。
此外,方差还可以看作是随机变量和自身的协方差。
在R中的代码实现:
# variance
x.var = sum((x - mean(x))^2)/(length(x)-1)
x.var
var(x)
标准差
标准差是一组数值自平均值分散开来的程度的一种测量观念。
总体的标准差
样本的标准差
在R中的代码实现:
# standard deviation
x.sd = sqrt(var(x))
x.sd
sd(x)
标准误
标准误差针对样本统计量而言,是某个样本统计量的标准差。当谈及标准误差时,一般须指明对应的样本统计量才有意义。以下以样本均值(样本均值是一种样本统计量)作为例子。于是,假设可以从总体中随机选取无限的大小相同的样本,那每个样本都可以有一个样本均值。依此法可以到一个由无限多样本均值组成的总体,该总体的标准差即为标准误差。
在R中的代码实现:
# standard error
x.se = sd(x)/sqrt(length(x))
x.se
协方差
协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。如果X与Y是统计独立的,那么二者之间的协方差就是0,但是反过来并不成立,即如果X与Y的协方差为0,二者并不一定是统计独立的。
协方差的相关性η(线性相关)
协方差的相关性η更准确地说是线性相关的相关系数r,是一个衡量线性独立的无量纲数,其取值在[-1,+1]之间。相关性η = 1时称为“完全线性相关”(相关性η = -1时称为“完全线性负相关”),此时将对作Y-X散点图,将得到一组精确排列在直线上的点;相关性数值介于-1到1之间时,其绝对值越接近1表明线性相关性越好,作散点图得到的点的排布越接近一条直线。相关性为0(因而协方差也为0)的两个随机变量又被称为是不相关的,或者更准确地说叫作“线性无关”、“线性不相关”,这仅仅表明X 与Y两随机变量之间没有线性相关性,并非表示它们之间一定没有任何内在的(非线性)函数关系,和前面所说的“X、Y二者并不一定是统计独立的”说法一致。
偏度skewness
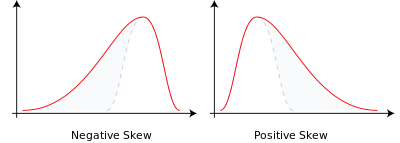
偏度衡量实数随机变量概率分布的不对称性。偏度的值可以为正,可以为负或者甚至是无法定义。在数量上,偏度为负(负偏态)就意味着在概率密度函数左侧的尾部比右侧的长,绝大多数的值(包括中位数在内)位于平均值的右侧。偏度为正(正偏态)就意味着在概率密度函数右侧的尾部比左侧的长,绝大多数的值(但不一定包括中位数)位于平均值的左侧。
随机变量X的偏度γ1:
具有n个值的样本的样本偏度g1:
在R中的代码实现:
# skewness
skewness = sum((x-mean(x))^3/sqrt(var(x))^3)/length(x); skewness
# 利用fBasics包
library(fBasics)
skewness(x, method = 'moment', na.rm = T)
峰度Kurtosis
峰度衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。 样本峰度g2:
为超值峰度(excess kurtosis)。“减3”是为了让正态分布的峰度为0
在R中的代码实现:
# kurtosis
## 这个公式手工计算居然不对,怎么也找不到原因,期待牛人指点
## kurtosis = sum((x-mean(x))^4)/(sum((x-mean(x))^2))^2 * length(x) -3; kurtosis
# 利用fBasics包
library(fBasics)
kurtosis(x, method = 'moment', na.rm = T)
无论偏度还是峰度都是和正态分布对比,即与正态分布的偏离程度。用的较多的为偏度值,正态分布的偏度值为0,大于0表示右偏,峰值在左,长尾在右,右边有很多极值存在,小于0则表示左偏,实际应用中偏度值在[-1,1]之间一般可以认为无偏。峰度值反应了陡峭程度,正态分布峰度值为0,大于0表示尖峰,小于0表示平峰。
后面的话
fBasics包中的basicStats函数可以对常用统计量进行快速计算。主要给出各个指标的基础信息和常用统计量,也可以比较全面的展现数据信息。nobs为观测值个数,NAs为缺失值个数,SE Mean为标准误均值,UCL\LCL Mean为95%置信水平下均值的上下限,Variance与Stdev为方差和标准差。
- - - - -
本文整理自维基百科。

