前话
简单线性回归用于计算两个连续型变量(如X，Y)之间的线性关系，具体地说就是计算下面公式中的。
其中称为残差,服从从的正态分布，自由度为(n-1) - (2-1) = n-2 为了找到这条直线的位置，我们使用最小二乘法(least squares approach)。最小二乘法确保所有点处的残差的平方和最小时计算，即下面示意图中有最小值。
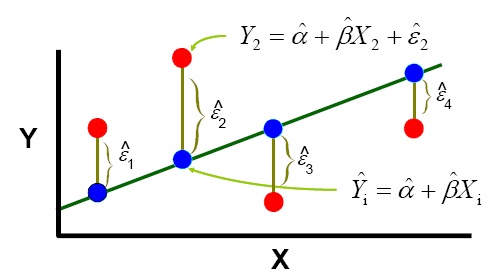
各指标的计算
运用最小二乘法找出的这条最优直线一定经过点。其中
斜率和截距的估计值
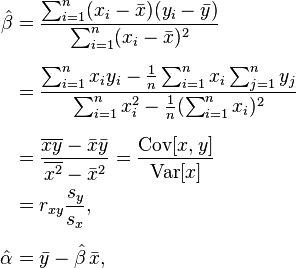
Pearson相关系数r
方差分析
在方差分析(ANOVA)中，总的平方和包含回归平方和残差平方和两部分。
- 总的平方和
其自由度为 n - 1，这里n为观测点的个数。
- 回归的平方和
其自由度为 2 - 1 = 1。
- 残差的平方和
其自由度为 (n -1) - (2 - 1) = n -2。
决定系数(拟合优势度)
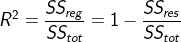决定系数是用来表示模型的解释度，理论上与相关系数没有关系，只是在简单线性回归中，决定系数$R^2 $值等于Pearson相关系数r的平方。
R中的实现
线性模拟
x = c(0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.20, 0.21, 0.23)
y = c(42.0, 43.5, 45.0, 45.5, 45.0, 47.5, 49.0, 53.0, 50.0, 55.0, 55.0, 60.0)
fit = lm(y ~ x)
summary(fit)
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## #Min 1Q Median 3Q Max
## -2.0431 -0.7056 0.1694 0.6633 2.2653
##
## Coefficients:
## #Estimate Std. Error t value Pr(>|t|)
## (Intercept) 28.493 1.580 18.04 5.88e-09 ***
## x 130.835 9.683 13.51 9.50e-08 ***
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
##
## Residual standard error: 1.319 on 10 degrees of freedom
## Multiple R-squared: 0.9481, Adjusted R-squared: 0.9429
## F-statistic: 182.6 on 1 and 10 DF, p-value: 9.505e-08
anova(fit)
##Analysis of Variance Table
##
##Response: y
## #Df Sum Sq Mean Sq F value Pr(>F)
##x 1 317.82 317.82 182.55 9.505e-08 ***
##Residuals 10 17.41 1.74
##---
##Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
线性模拟各参数的提取
# 可以通过names函数查看summary(fit)中个具体参数的提取方法
names(summary(fit))
# 提取R square
summary(fit)$r.squared ## 依照该形式可以提取names(summary(fit))中任意指标
# 其它常用指标的提取
# 提取模型lm或glm提取回归系数
coefficients(fit)
# 还可简化为
coef(fit)
# 提取模型lm或glm的残差
# 也可简化为
residuals(fit)
resid(fit)
# 提取lm或glm对象中残差的平方和
deviance(fit)
# 提取lm或glm对象中的方差分析表
# 其中p值越小，差异越显著, beita1越不可能为0
anova(fit)
# 预测数据
new <- data.frame(x=c(0.16, 2.3))
predict(fit, new)
## 也可以做出预测区间
predict(fit, new, interval = 'prediction', levels = 0.95)
线性模拟各参数中各量的算法
五个和的计算
## 预备统计量(Sums of square and sums of producte)
Sx = sum(x)
Sy = sum(y)
Sxx = sum((x - mean(x))^2)
Syy = sum((y - mean(y))^2)
Sxy = sum((x - mean(x)) * (y - mean(y)))
## 这里仅仅作为补充,具体原因不是很清楚
Syy = deviance(lm(y~1))
n = length(x)
回归系数
## 回归系数$\alpha$和$beta$（这样计算，residuals有最小值)
beta = Sxy/Sxx
beta
alpha = mean(y) - beta*mean(x)
alpha
# 提取lm或glm对象中的回归系数
coef(fit)
残差及五分位数
residuals = y - (beta + alpha * x)
residuals
quantile(residuals)
# 提取模型lm或glm的残差
# 也可简化为
residuals(fit)
Pearson相关系数r
r = sqrt(Sxy/(Sxx * Syy))
r
R平方
决定系数，其值为 回归的平方和/总的平方和。
rsquare = (Syy - sum(residuals^2))/Syy
rsquare
adjust R平方
## 考虑到了自变量的个数, 包括截距在内, 本例子中k = 2
n = length(x)
k = 2
adjustrsquare = 1- (1-rsquare)*(n-1)/(n-k)
adjustrsquare
回归方程的F检验
在简单线性回归的模型，我们可以在时，对F统计量进行检验。 在F检验中统计量F
对应p值越小，说明此时越小的概率时间发生了，越不能接受原假设。
斜率β的t检验
在简单线性回归的模型，我们可以检验回归系数(斜率)β是否相等于特定的$β_0$(通常使$β_0 = 0$以检验$x_i$对$y_i$是否有关联)。 统计量t
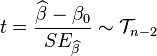在零假设为$β = β_0$的情况下服从自由度为n − 2之t分布，其中
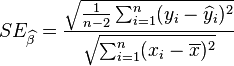同F检验一样，p值越小，说明此时越小的概率事件发生了，越不能接受原假设。
话外篇
在R中，lm(y ~ x)和lm(y ~ x + 1)的效果是相同的。此外，lm(y ~ 1)中截距的估计值为y的平均值，残差为每个y与均值的离差。